Leyes de Newton

La primera y segunda ley de Newton, en latín, en la edición original de su obra Principia Mathematica

Las leyes de Newton, también conocidas como leyes del movimiento de Newton,¹ son tres principios a partir de los cuales se explican una gran parte de los problemas planteados en mecánica clásica, en particular aquellos relativos al movimiento de los cuerpos, que revolucionaron los conceptos básicos de la física y el movimiento de los cuerpos en el universo.

Constituyen los cimientos no solo de la dinámica clásica sino también de la física clásica en general. Aunque incluyen ciertas definiciones y en cierto sentido pueden verse como axiomas, Newton afirmó que estaban basadas en observaciones y experimentos cuantitativos; ciertamente no pueden derivarse a partir de otras relaciones más básicas. La demostración de su validez radica en sus predicciones... La validez de esas predicciones fue verificada en todos y cada uno de los casos durante más de dos siglos.²

En concreto, la relevancia de estas leyes radica en dos aspectos: por un lado constituyen, junto con la transformación de Galileo, la base de la mecánica clásica, y por otro, al combinar estas leyes con la ley de la gravitación universal, se pueden deducir y explicar las leyes de Kepler sobre el movimiento planetario. Así, las leyes de Newton permiten explicar, por ejemplo, tanto el movimiento de los astros como los movimientos de los proyectiles artificiales creados por el ser humano y toda la mecánica de funcionamiento de las máquinas. Su formulación matemática fue publicada por Isaac Newton en 1687 en su obra Philosophiæ naturalis principia mathematica.^{nota 1}
La dinámica de Newton, también llamada dinámica clásica, solo se cumple en los sistemas de referencia inerciales (que se mueven a velocidad constante; la Tierra, aunque gire y rote, se trata como tal a efectos de muchos experimentos prácticos). Solo es aplicable a cuerpos cuya velocidad dista considerablemente de la velocidad de la luz; cuando la velocidad del cuerpo se va aproximando a los 300 000 km/s (lo que ocurriría en los sistemas de referencia no-inerciales) aparecen una serie de fenómenos denominados efectos relativistas. El estudio de estos efectos (aumento de la masa y contracción de la longitud, fundamentalmente) corresponde a la teoría de la relatividad especial, enunciada por Albert Einstein en 1905.

Índice

• 1 Historia
• 2 Fundamentos teóricos de las leyes
• 3 Primera ley de Newton o ley de inercia
  • 3.1 Sistemas de referencia inerciales
  • 3.2 Aplicación de la primera ley de Newton
• 4 Segunda ley de Newton o ley fundamental de la dinámica
  • 4.1 Si la masa es constante
  • 4.2 Si la masa no es constante
  • 4.3 Cantidad de movimiento o momento lineal
  • 4.4 Aplicaciones de la segunda ley de Newton
• 5 Tercera ley de Newton o principio de acción y reacción
  • 5.1 Aplicaciones de la Tercera Ley de Newton
• 6 Limitaciones y generalizaciones posteriores
  • 6.1 Generalizaciones relativistas
  • 6.2 Teorema de Ehrenfest
• 7 Véase también
• 8 Notas
• 9 Referencias
• 10 Bibliografía
• 11 Enlaces externos

Historia

Busto de Aristóteles

La dinámica es la parte de la física que estudia las relaciones entre los movimientos de los cuerpos y las causas que los provocan, en concreto las fuerzas que actúan sobre ellos. La dinámica, desde el punto de vista de la mecánica clásica, es apropiada para el estudio dinámico de sistemas grandes en comparación con los átomos y que se mueven a velocidades mucho menores que las de la luz.³ Para entender estos fenómenos, el punto de partida es la observación del mundo cotidiano. Si se desea cambiar la posición de un cuerpo en reposo es necesario empujarlo o levantarlo, es decir, ejercer una acción sobre él.
Aparte de estas intuiciones básicas, el problema del movimiento es muy complejo: todos aquellos que se observan en la naturaleza (caída de un objeto en el aire, movimiento de una bicicleta, un coche o un cohete espacial) son complicados. Esto motivó que el conocimiento sobre estos hechos fuera erróneo durante siglos. Aristóteles pensó que el movimiento de un cuerpo se detiene cuando la fuerza que lo empuja deja de actuar. Posteriormente se descubrió que esto no era cierto pero el prestigio de Aristóteles como filósofo y científico hizo que estas ideas perduraran siglos,^{nota 2 4} hasta que científicos como Galileo Galilei o Isaac Newton hicieron avances muy importantes con sus nuevas formulaciones. Sin embargo hubo varios físicos que se aproximaron de manera muy certera a las formulaciones de Newton mucho antes de que este formulara sus leyes del movimiento.

Busto de Domingo de Soto en Segovia

Es el caso del español Juan de Celaya,⁵ matemático, físico, cosmólogo, teólogo y filósofo que en 1517 publicó un tratado titulado In octo libros physicorum Aristotelis cum quaestionibus eiusdem, secundum triplicem viam beati Thomae, realium et nominatium, obra de especial interés para el estudio de los orígenes de la moderna ciencia del movimiento. Durante su etapa en Francia fue un escritor prolífico, escribiendo sobre todo acerca de la física de Aristóteles y el movimiento. También publicó numerosos trabajos sobre filosofía y lógica. Fue uno de los impulsores de la lógica nominalista y de las ideas mertonianas de los calculatores acerca de la dinámica. Fue capaz de enunciar, dentro de las Leyes de Newton, la Primera Ley de o Primer Principio de la Dinámica (una de las leyes más importantes de la física) un siglo antes que Newton.⁶
Otro destacado pionero fue el también español, y discípulo de Celaya, Domingo de Soto,⁷ fraile dominico y teólogo considerado como el promotor de la física moderna.⁸ Su teoría del movimiento uniformemente acelerado y la caída de los graves fue el precedente de la Ley de la Gravedad de Newton. Escribió numerosas obras de teología, derecho, filosofía y lógica y también comentó varios libros de física y lógica aristotélica, de los cuales el más importante fue Quaestiones super octo libros physicorum Aristotelis (1551), sobre cinemática y dinámica, la cual fue publicada en varias ciudades italianas, influyendo en personajes como Benedetti o Galileo. Domingo de Soto fue uno de los primeros en establecer que un cuerpo en caída libre sufre una aceleración uniforme con respecto al tiempo —dicha afirmación también había sido establecida por Nicolás Oresme casi dos siglos antes— y su concepción sobre la masa fue avanzada en su época. En su libro Quaestiones explica la aceleración constante de un cuerpo en caída libre de esta manera:

Este tipo de movimiento propiamente sucede en los graves naturalmente movidos y en los proyectiles. Donde un peso cae desde lo alto por un medio uniforme, se mueve más veloz en el fin que en el principio. Sin embargo el movimiento de los proyectiles es más lento al final que al principio: el primero aumenta de modo uniformemente disforme, y el segundo en cambio disminuye de modo uniformemente disforme.⁹

Domingo de Soto ya relacionaba dos aspectos de la física: el movimiento uniformemente disforme (movimiento uniformemente acelerado) y la caída de graves (resistencia interna). En su teoría combinaba la abstracción matemática con la realidad física, clave para la comprensión de las leyes de la naturaleza. Tenía una claridad rotunda acerca de este hecho y lo expresaba en ejemplos numéricos concretos. Clasificó los diferentes tipos de movimiento en:^{8 nota 3}

• Movimiento uniforme respecto al tiempo:

Es aquel por el que el mismo móvil en iguales intervalos de tiempo recorre iguales distancias, como se da perfectamente en el movimiento extremadamente regular del cielo.

• Movimiento disforme con respecto al tiempo:

Es aquel por el cual, en partes iguales de tiempo son recorridas distancias desiguales, o en (tiempos) desiguales, (espacios) iguales.

• Movimiento uniformemente disforme con respecto al tiempo:

Es el movimiento de tal modo disforme, que si dividimos según el tiempo, (la velocidad de) el punto medio de la proporción excede (la velocidad de) el extremo más lento lo que es excedida por el más rápido.

El movimiento uniformemente disforme respecto al tiempo es aquel cuya diformidad es tal, que si se le divide según el tiempo, es decir, según las partes que se suceden en el tiempo, en cada parte del movimiento del punto central excede del movimiento extremo el menor de esa misma parte en cantidad igual a aquella en la que él mismo es superado por el movimiento extremo más intenso.

Soto describió el movimiento de caída libre como ejemplo de movimiento uniformemente acelerado por primera vez, cuestión que solo aparecerá posteriormente en la obra de Galileo:^{8 nota 4}

...este tipo de movimiento propiamente sucede en los (graves) naturalmente movidos y en los proyectiles. Donde un peso cae desde lo alto por un medio uniforme, se mueve más veloz en el fin que en el principio. Sin embargo el movimiento de los proyectiles es más lento al final que al principio: el primero aumenta de modo uniformemente disforme, y el segundo en cambio disminuye de modo uniformemente diforme.

Por lo tanto era aplicable la ley de la velocidad media para calcular el tiempo de caída:

Esta especie de movimiento es la propia de los cuerpos que se mueven con movimiento natural y la de los proyectiles.

En efecto, cada vez que cae una masa desde una cierta altura y en el seno de un medio homogéneo, se mueve al final más de prisa que al principio. Pero el movimiento de los proyectiles es más lento al final que al comienzo, y así el primero se intensifica, y el segundo se debilita uniformemente.

Movimiento diformente disforme con respecto al tiempo:

Es el movimiento en tal modo disforme, que si es dividido según el tiempo, no ocurre que el punto medio de cada parte en la misma proporción excede (en velocidad) a un extremo cuanto es excedido por el otro. Este tipo de movimiento es el que esperamos en los animales, donde se observa el aumento y la disminución.

Retrato de Galileo Galilei

Este fue un descubrimiento clave en física y base esencial para el posterior estudio de la gravedad por Galileo Galilei e Isaac Newton. Ningún científico de las universidades de París y Oxford de aquella época había conseguido describir la relación entre movimiento uniformemente disforme en el tiempo y la caída de los graves como lo hizo Soto.
Tras las ideas innovadoras sobre el movimiento de estos científicos, Galileo hizo un avance muy importante al introducir el método científico que enseña que no siempre se debe creer en las conclusiones intuitivas basadas en la observación inmediata, pues esto lleva a menudo a equivocaciones. Galileo realizó un gran número de experiencias en las que se iban cambiando ligeramente las condiciones del problema y midió los resultados en cada caso. De esta manera pudo extrapolar sus observaciones hasta llegar a entender un experimento ideal.^{3 nota 5} En concreto, observó cómo un cuerpo que se mueve con velocidad constante sobre una superficie lisa se moverá eternamente si no hay rozamientos ni otras acciones externas sobre él.
Inmediatamente se presentó otro problema: ¿si la velocidad no lo revela, qué parámetro del movimiento indica la acción de fuerzas exteriores?; Galileo respondió también a esta pregunta, pero Newton lo hizo de manera más precisa: no es la velocidad sino su variación la consecuencia resultante de la acción de arrastrar o empujar un objeto. Esta relación entre fuerza y cambio de velocidad (aceleración) constituye la base fundamental de la mecánica clásica. Fue Isaac Newton (hacia 1690) el primero en dar una formulación completa de las leyes de la mecánica e inventó los procedimientos matemáticos necesarios para explicarlos y obtener información a partir de ellos.^{3 nota 6}

Fundamentos teóricos de las leyes

Retrato de Sir Isaac Newton (1642-1727)

El primer concepto que maneja Newton es el de masa, que identifica con «cantidad de materia». Newton asume a continuación que la cantidad de movimiento es el resultado del producto de la masa por la velocidad. En tercer lugar, precisa la importancia de distinguir entre lo absoluto y relativo siempre que se hable de tiempo, espacio, lugar o movimiento.
En este sentido, Newton, que entiende el movimiento como una traslación de un cuerpo de un lugar a otro, para llegar al movimiento absoluto y verdadero de un cuerpo:

compone el movimiento (relativo) de ese cuerpo en el lugar (relativo) en que se lo considera, con el movimiento (relativo) del lugar mismo en otro lugar en el que esté situado, y así sucesivamente, paso a paso, hasta llegar a un lugar inmóvil, es decir, al sistema de referencias de los movimientos absolutos.¹⁰

De acuerdo con esto, establece que los movimientos aparentes son las diferencias de los movimientos verdaderos y que las fuerzas son causas y efectos de estos. Consecuentemente, la fuerza en Newton tiene un carácter absoluto, no relativo.
Las leyes enunciadas por Newton, y consideradas como las más importantes de la mecánica clásica, son tres: la ley de inercia, la relación entre fuerza y aceleración y la ley de acción y reacción. Newton planteó que todos los movimientos se atienen a estas tres leyes principales, formuladas en términos matemáticos. Un concepto es la fuerza, causa del movimiento y otro es la masa, la medición de la cantidad de materia puesta en movimiento; los dos son denominados habitualmente por las letras F y m.

Primera ley de Newton o ley de inercia

La primera ley del movimiento rebate la idea aristotélica de que un cuerpo solo puede mantenerse en movimiento si se le aplica una fuerza. Newton expone que:

Corpus omne perseverare in statu suo quiescendi vel movendi uniformiter in directum, nisi quatenus illud a viribus impressis cogitur statum suum mutare.11

Todo cuerpo persevera en su estado de reposo o movimiento uniforme y rectilíneo a no ser que sea obligado a cambiar su estado por fuerzas impresas sobre él.12

Esta ley postula, por tanto, que un cuerpo no puede cambiar por sí solo su estado inicial, ya sea en reposo o en movimiento rectilíneo uniforme, a menos que se aplique una fuerza o una serie de fuerzas cuya resultante no sea nula. Newton toma en consideración, así, el que los cuerpos en movimiento están sometidos constantemente a fuerzas de roce o fricción, que los frena de forma progresiva, algo novedoso respecto de concepciones anteriores que entendían que el movimiento o la detención de un cuerpo se debía exclusivamente a si se ejercía sobre ellos una fuerza, pero nunca entendiendo como tal a la fricción.
En consecuencia, un cuerpo que se desplaza con movimiento rectilíneo uniforme implica que no existe ninguna fuerza externa neta o, dicho de otra forma, un objeto en movimiento no se detiene de forma natural si no se aplica una fuerza sobre él. En el caso de los cuerpos en reposo, se entiende que su velocidad es cero, por lo que si esta cambia es porque sobre ese cuerpo se ha ejercido una fuerza neta.
Newton descubrió la ley de la inercia, la tendencia de un objeto en movimiento a continuar moviéndose en una línea recta, a menos que sufra la influencia de algo que le desvíe de su camino. Newton supuso que si la Luna no salía disparada en línea recta, según una línea tangencial a su órbita, se debía a la presencia de otra fuerza que la empujaba en dirección a la Tierra, y que desviaba constantemente su camino convirtiéndolo en un círculo. Newton llamó a esta fuerza gravedad y creyó que actuaba a distancia. No hay nada que conecte físicamente la Tierra y la Luna y sin embargo la Tierra está constantemente tirando de la Luna hacia nosotros. Newton se sirvió de la tercera ley de Kepler y dedujo matemáticamente la naturaleza de la fuerza de la gravedad. Demostró que la misma fuerza que hacía caer una manzana sobre la Tierra mantenía a la Luna en su órbita.
La primera ley de Newton establece la equivalencia entre el estado de reposo y de movimiento rectilíneo uniforme. Supongamos un sistema de referencia S y otro S´ que se desplaza respecto del primero a una velocidad constante. Si sobre una partícula en reposo en el sistema S´ no actúa una fuerza neta, su estado de movimiento no cambiará y permanecerá en reposo respecto del sistema S´ y con movimiento rectilíneo uniforme respecto del sistema S. La primera ley de Newton se satisface en ambos sistemas de referencia. A estos sistemas en los que se satisfacen las leyes de Newton se les da el nombre de sistemas de referencia inerciales. Ningún sistema de referencia inercial tiene preferencia sobre otro sistema inercial, son equivalentes: este concepto constituye el principio de relatividad de Galileo o newtoniano.
El enunciado fundamental que podemos extraer de la ley de Newton es que la ${\displaystyle {\vec {F}}=m\cdot {\vec {a}}}$. Esta expresión es una ecuación vectorial, ya que tanto la fuerza como la aceleración llevan dirección y sentido. Por otra parte, cabe destacar que la aceleración no es la variación de la posición, sino que es la variación con la que varía la velocidad.
De la ecuación ${\displaystyle {\vec {F}}=m\cdot {\vec {a}}}$ podemos deducir que si actúan fuerzas sobre los cuerpos, el cambio que se provoca en su aceleración es proporcional a la fuerza aplicada y dicho cambio se produce en la dirección sobre la que se apliquen dichas fuerzas.

Sistemas de referencia inerciales

Artículo principal: Sistema de referencia inercial

La primera ley de Newton sirve para definir un tipo especial de sistemas de referencia conocidos como sistemas de referencia inerciales, que son aquellos desde los que se observa que un cuerpo sobre el que no actúa ninguna fuerza neta se mueve con velocidad constante.
Un sistema de referencia con aceleración (y la aceleración normal de un sistema rotatorio se incluye en esta definición) no es un sistema inercial, y la observación de una partícula en reposo en el propio sistema no satisfará las leyes de Newton (puesto que se observará aceleración sin la presencia de fuerza neta alguna). Se denominan sistemas de referencia no inerciales.

Diferencia de planteamiento de un problema debido a la posibilidad de observarlo desde dos puntos de vista: el punto de vista de un observador externo (inercial) o desde un observador interno

Por ejemplo considérese una plataforma girando con velocidad constante, ω, en la que un objeto está atado al eje de giro mediante una cuerda, y supongamos dos observadores, uno inercial externo a la plataforma y otro no inercial situado sobre ella.³

• Observador inercial: desde su punto de vista el bloque se mueve en círculo con velocidad v y está acelerado hacia el centro de la plataforma con una aceleración centrípeta ${\displaystyle a={v^{2} \over r}}$. Esta aceleración es consecuencia de la fuerza ejercida por la tensión de la cuerda.
• Observador no inercial: para el observador que gira con la plataforma el objeto está en reposo, a = 0. Es decir, observa una fuerza ficticia que contrarresta la tensión para que no haya aceleración centrípeta. Esa fuerza debe ser ${\displaystyle F_{c}={mv^{2} \over r}}$. Este observador siente la fuerza como si fuera perfectamente real, aunque solo sea la consecuencia de la aceleración del sistema de referencia en que se encuentra.

En realidad, es imposible encontrar un sistema de referencia inercial, ya que siempre hay algún tipo de fuerzas actuando sobre los cuerpos; no obstante, siempre es posible encontrar un sistema de referencia en el que el problema que estemos estudiando se pueda tratar como si estuviésemos en un sistema inercial. En muchos casos, la Tierra es una buena aproximación de sistema inercial, ya que a pesar de contar con una aceleración traslacional y otra rotacional, ambas son del orden de 0.01 ${\displaystyle m \over s^{2}}$ y, en consecuencia, podemos considerar que un sistema de referencia de un observador en la superficie terrestre es un sistema de referencia inercial.

Aplicación de la primera ley de Newton

Se puede considerar como ejemplo ilustrativo de esta primera ley una bola atada a una cuerda, de modo que la bola gira siguiendo una trayectoria circular. Debido a la fuerza centrípeta de la cuerda (tensión), la masa sigue la trayectoria circular, pero si en algún momento la cuerda se rompiese, la bola tomaría una trayectoria rectilínea en la dirección de la velocidad que tenía la bola en el instante de rotura.

Tras la rotura, la fuerza neta ejercida sobre la bola es 0, por lo que experimentará, como resultado de un estado de reposo, un movimiento rectilíneo uniforme.

Segunda ley de Newton o ley fundamental de la dinámica

La Segunda Ley de Newton expresa que:

Mutationem motus proportionalem esse vi motrici impressæ, & fieri secundum lineam rectam qua vis illa imprimitur.11

El cambio de movimiento es directamente proporcional a la fuerza motriz impresa y ocurre según la línea recta a lo largo de la cual aquella fuerza se imprime.13

Esta ley se encarga de cuantificar el concepto de fuerza. La aceleración que adquiere un cuerpo es proporcional a la fuerza neta aplicada sobre el mismo. La constante de proporcionalidad es la masa del cuerpo (que puede ser o no ser constante). Entender la fuerza como la causa del cambio de movimiento y la proporcionalidad entre la fuerza impresa y el cambio de la velocidad de un cuerpo es la esencia de esta segunda ley.¹⁴

Si la masa es constante

Si la masa del cuerpo es constante se puede establecer la siguiente relación, que constituye la ecuación fundamental de la dinámica:

${\displaystyle {\overrightarrow {F}}_{\rm {resultante}}=m\cdot {\vec {a}}}$

Donde m es la masa del cuerpo la cual debe ser constante para ser expresada de tal forma. La fuerza neta que actúa sobre un cuerpo, también llamada fuerza resultante, es el vector suma de todas las fuerzas que sobre él actúan. Así pues:¹⁵

${\displaystyle \sum _{i=1}^{n}{\overrightarrow {F_{i}}}=m\cdot {\vec {a}}}$

• La aceleración que adquiere un cuerpo es proporcional a la fuerza aplicada, y la constante de proporcionalidad es la masa del cuerpo.
• Si actúan varias fuerzas, esta ecuación se refiere a la fuerza resultante, suma vectorial de todas ellas.
• Esta es una ecuación vectorial, luego se debe cumplir componente a componente.
• En ocasiones será útil recordar el concepto de componentes intrínsecas: si la trayectoria no es rectilínea es porque hay una aceleración normal, luego habrá también una fuerza normal (en dirección perpendicular a la trayectoria); si el módulo de la velocidad varía es porque hay una aceleración en la dirección de la velocidad (en la misma dirección de la trayectoria).
• La fuerza y la aceleración son vectores paralelos, pero esto no significa que el vector velocidad sea paralelo a la fuerza. Es decir, la trayectoria no tiene por qué ser tangente a la fuerza aplicada (sólo ocurre si al menos, la dirección de la velocidad es constante).
• Esta ecuación debe cumplirse para todos los cuerpos. Cuando analicemos un problema con varios cuerpos y diferentes fuerzas aplicadas sobre ellos, deberemos entonces tener en cuenta las fuerzas que actúan sobre cada uno de ellos y el principio de superposición de fuerzas. Aplicaremos la segunda ley de Newton para cada uno de ellos, teniendo en cuenta las interacciones mutuas y obteniendo la fuerza resultante sobre cada uno de ellos.

Representación del sumatorio de las fuerzas. Aquí se está sumando dos veces la fuerza No. 2. La resultante (marcada con rojo) responde a la siguiente ecuación: ${\displaystyle {\overrightarrow {F}}_{\rm {resultante}}={\overrightarrow {F_{1}}}+2\cdot {\overrightarrow {F_{2}}}+{\overrightarrow {F_{3}}}}$

El principio de superposición establece que si varias fuerzas actúan igual o simultáneamente sobre un cuerpo, la fuerza resultante es igual a la suma vectorial de las fuerzas que actúan independientemente sobre el cuerpo (regla del paralelogramo). Este principio aparece incluido en los Principia de Newton como Corolario 1, después de la tercera ley, pero es requisito indispensable para la comprensión y aplicación de las leyes, así como para la caracterización vectorial de las fuerzas.¹⁴ La fuerza modificará el estado de movimiento, cambiando la velocidad en módulo o dirección. Las fuerzas son causas que producen aceleraciones en los cuerpos. Por lo tanto existe una relación causa-efecto entre la fuerza aplicada y la aceleración que se este cuerpo experimenta.
De esta ecuación se obtiene la unidad de medida de la fuerza en el Sistema Internacional de Unidades, el Newton:

${\displaystyle {\rm {1\,N=1\;{{kg\cdot m} \over s^{2}}}}}$

Por otro lado, si la fuerza resultante que actúa sobre una partícula no es cero, esta partícula tendrá una aceleración proporcional a la magnitud de la resultante y en dirección de esta (debido a que la masa siempre es un escalar positivo). La expresión anterior así establecida es válida tanto para la mecánica clásica como para la mecánica relativista (la dinámica clásica afirma que la masa de un cuerpo es siempre la misma, con independencia de la velocidad con la que se mueve, la mecánica relativista establece que la masa de un cuerpo aumenta al crecer la velocidad).

Si la masa no es constante

Si la masa de los cuerpos varia, como por ejemplo un cohete que va quemando combustible, no es válida la relación ${\displaystyle F=m\cdot a}$ y hay que hacer genérica la ley para que incluya el caso de sistemas en los que pueda variar la masa. Para ello primero hay que definir una magnitud física nueva, la cantidad de movimiento, que se representa por la letra p y que se define como el producto de la masa de un cuerpo por su velocidad, es decir:

${\displaystyle {\vec {P}}=m\cdot {\vec {v}}}$

Newton enunció su ley de una forma más general:

${\displaystyle {\overrightarrow {F}}_{\rm {neta}}={d(m~{\vec {v}}) \over dt}}$

De esta forma se puede relacionar la fuerza con la aceleración y con la masa, sin importar que esta sea o no sea constante. Cuando la masa es constante sale de la derivada con lo que queda la expresión:

${\displaystyle {\overrightarrow {F}}_{\rm {neta}}=m{d({\vec {v}}) \over dt}}$

Y se obtiene la expresión clásica de la Segunda Ley de Newton:

${\displaystyle {\overrightarrow {F}}_{\rm {neta}}=m\cdot {\vec {a}}}$

La fuerza, por lo tanto, es un concepto matemático el cual, por definición, es igual a la derivada con respecto al tiempo del momento de una partícula dada, cuyo valor a su vez depende de su interacción con otras partículas. Por consiguiente, se puede considerar la fuerza como la expresión de una interacción. Otra consecuencia de expresar la Segunda Ley de Newton usando la cantidad de movimiento es lo que se conoce como principio de conservación de la cantidad de movimiento: si la fuerza total que actúa sobre un cuerpo es cero, la Segunda ley de Newton nos dice que

${\displaystyle {\vec {0}}={d{\vec {p}} \over dt}}$

Es decir, la derivada de la cantidad de movimiento con respecto al tiempo es cero en sus tres componentes. Esto significa que la cantidad de movimiento debe ser constante en el tiempo en módulo dirección y sentido (la derivada de un vector constante es cero).¹⁶
La segunda ley de Newton solo es válida en sistemas de referencia inerciales pero incluso si el sistema de referencia es no inercial, se puede utilizar la misma ecuación incluyendo las fuerzas ficticias (o fuerzas inerciales). Unidades y dimensiones de la fuerza:

• Unidades S.I.: ${\displaystyle {\rm {Newton={kg\cdot m \over s^{2}}}}}$
• Sistema cegesimal: dina
• Equivalencia: 1 N= ${\displaystyle 10^{5}}$ dinas

Cantidad de movimiento o momento lineal

En el lenguaje moderno la cantidad de movimiento o momento lineal de un objeto se define mediante la expresión ${\displaystyle {\vec {p}}={m\cdot {\vec {v}}}}$. Es decir, es una magnitud vectorial proporcional a la masa y a la velocidad del objeto. Partiendo de esta definición y aplicando la ley fundamental de la mecánica de Newton, las variaciones de la cantidad de movimiento se expresan en función de la fuerza resultante y el intervalo de tiempo durante el cual se ejerce esta:

${\displaystyle {\overrightarrow {F}}_{\rm {result}}=m\cdot {\vec {a}}=m{d({\vec {v}}) \over dt}}$

${\displaystyle {\overrightarrow {F}}_{\rm {result}}\cdot dt=m\cdot d{\vec {v}}={d(m\cdot {\vec {v}})}=d{\vec {p}}}$

Al vector ${\displaystyle {\overrightarrow {F}}_{\rm {result}}\cdot dt}$ se le denomina impulso lineal y representa una magnitud física que se manifiesta especialmente en las acciones rápidas o impactos, tales como choques, llevando módulo dirección y sentido. En este tipo de acciones conviene considerar la duración del impacto y la fuerza ejercida durante el mismo.
De la expresión obtenida se deduce que el impulso lineal es igual a la variación de la cantidad de movimiento. Si la fuerza resultante es cero (es decir, si no se actúa sobre el objeto) el impulso también es cero y la cantidad de movimiento permanece constante. Llamamos a esta afirmación ley de conservación del impulso lineal, aplicada a un objeto o una partícula.¹⁷
Sus unidades en el Sistema Internacional son ${\displaystyle {\rm {kg\cdot m \over s}}}$

Conservación de la cantidad de movimiento

Bolas representando choque elástico

• Choque elástico: permanecen constantes la cantidad de movimiento y la energía cinética. Dos partículas de masas diferentes que solo interactúan entre sí y que se mueven con velocidades constantes y distintas una hacia la otra. Tras el choque, permanece constante la cantidad de movimiento y la energía cinética.

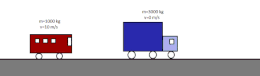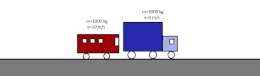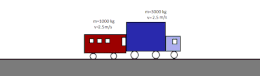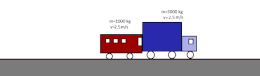
Coches representando choque inelástico

• Choque inelástico: permanece constante la cantidad de movimiento y varía la energía cinética. Como consecuencia, los cuerpos que colisionan pueden sufrir deformaciones y aumento de su temperatura. Tras un choque totalmente inelástico, ambos cuerpos tienen la misma velocidad. La suma de sus energías cinéticas es menor que la inicial porque una parte de esta se ha transformado en energía interna; en la mayoría de los casos llega a ser disipada en forma de calor debido al calentamiento producido en el choque. En el caso ideal de un choque perfectamente inelástico entre objetos macroscópicos, estos permanecen unidos entre sí tras la colisión.¹⁸

Aplicaciones de la segunda ley de Newton

Entre las posibles aplicaciones de la Segunda Ley de Newton, se pueden destacar:

• Caída libre: es un movimiento que se observa cuando un objeto se deja caer desde una cierta altura sobre la superficie de la tierra. Para estudiar el movimiento se elige un sistema de coordenadas donde el origen del eje y está sobre esta última. En este sistema tanto la velocidad de caída como la aceleración de la gravedad tienen signo negativo. En el ejemplo representado, se supone que el objeto se deja caer desde el reposo, pero es posible que caiga desde una velocidad inicial distinta de cero.¹⁸

Péndulo Simple: Diagrama de Fuerzas

• Péndulo simple: partícula de masa m suspendida del punto O por un hilo inextensible de longitud l y de masa despreciable. Si la partícula se desplaza a una posición θ₀ (ángulo que hace el hilo con la vertical) y luego se suelta, el péndulo comienza a oscilar. El péndulo describe una trayectoria circular, un arco de una circunferencia de radio l. Las fuerzas que actúan sobre la partícula de masa m son dos, el peso y la tensión T del hilo.

Si se aplica la segunda ley, en la dirección radial:

${\displaystyle m\cdot a_{n}=T-mg\cdot \cos {\theta }}$

donde a_n representa la aceleración normal a la trayectoria. Conocido el valor de la velocidad v en la posición angular se puede determinar la tensión T del hilo. Esta es máxima cuando el péndulo pasa por la posición de equilibrio

${\displaystyle T=mg+{{m\cdot v^{2}} \over {l}}}$

,
donde el segundo término representa la fuerza centrífuga.
Y la tensión es mínima, en los extremos de su trayectoria, cuando la velocidad es cero

${\displaystyle T=mg\cdot \cos {\theta }}$

en la dirección tangencial:

${\displaystyle m\cdot a_{t}=-mg\cdot \operatorname {sen} {\theta }}$

donde a_t representa la aceleración tangente a la trayectoria.

Tercera ley de Newton o principio de acción y reacción

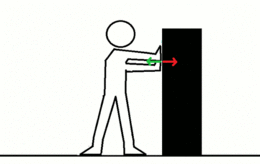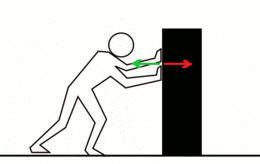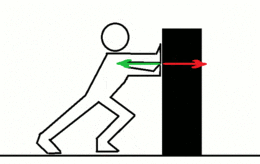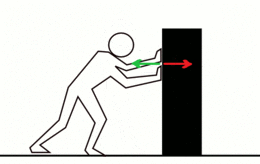
La tercera ley de Newton establece que siempre que un objeto ejerce una fuerza sobre un segundo objeto, este ejerce una fuerza de igual magnitud y dirección pero en sentido opuesto sobre el primero. Con frecuencia se enuncia así: A cada acción siempre se opone una reacción igual pero de sentido contrario. En cualquier interacción hay un par de fuerzas de acción y reacción situadas en la misma dirección con igual magnitud y sentidos opuestos. La formulación original de Newton es:

Actioni contrariam semper & æqualem esse reactionem: sive corporum duorum actiones in se mutuo semper esse æquales & in partes contrarias dirigi.11

Con toda acción ocurre siempre una reacción igual y contraria: quiere decir que las acciones mutuas de dos cuerpos siempre son iguales y dirigidas en sentido opuesto.13

Esta tercera ley de Newton es completamente original (pues las dos primeras ya habían sido propuestas de otra manera por Galileo, Hooke y Huygens) y hace de las leyes de la mecánica un conjunto lógico y completo.¹⁹ Expone que por cada fuerza que actúa sobre un cuerpo, este realiza una fuerza de igual intensidad, pero de sentido contrario sobre el cuerpo que la produjo. Dicho de otra forma, las fuerzas, situadas sobre la misma recta, siempre se presentan en pares de igual magnitud y de dirección, pero con sentido opuesto. Si dos objetos interaccionan, la fuerza F₁₂, ejercida por el objeto 1 sobre el objeto 2, es igual en magnitud con misma dirección pero sentidos opuestos a la fuerza F₂₁ ejercida por el objeto 2 sobre el objeto 1:²⁰
${\displaystyle {\vec {F}}_{12}=-{\vec {F}}_{21}}$ Este principio presupone que la interacción entre dos partículas se propaga instantáneamente en el espacio (lo cual requeriría velocidad infinita), y en su formulación original no es válido para fuerzas electromagnéticas puesto que estas no se propagan por el espacio de modo instantáneo sino que lo hacen a velocidad finita "c". Este principio relaciona dos fuerzas que no están aplicadas al mismo cuerpo, produciendo en ellos aceleraciones diferentes, según sean sus masas. Por lo demás, cada una de esas fuerzas obedece por separado a la segunda ley. Junto con las anteriores leyes, esta permite enunciar los principios de conservación del momento lineal y del momento angular.¹⁴

La fuerza de reacción (flecha verde) aumenta conforme aumenta la aplicada al objeto, la fuerza aplicada (flecha roja)

Aplicaciones de la Tercera Ley de Newton

Algunos ejemplos donde actúan las fuerzas acción-reacción son los siguientes:²⁰

• Si una persona empuja a otra de peso similar, las dos se mueven con la misma velocidad pero en sentido contrario.
• Cuando saltamos, empujamos a la tierra hacia abajo, que no se mueve debido a su gran masa, y esta nos empuja con la misma intensidad hacia arriba.
• Una persona que rema en un bote empuja el agua con el remo en un sentido y el agua responde empujando el bote en sentido opuesto.
• Cuando caminamos empujamos a la tierra hacia atrás con nuestros pies, a lo que la tierra responde empujándonos a nosotros hacia delante, haciendo que avancemos.
• Cuando se dispara una bala, la explosión de la pólvora ejerce una fuerza sobre la pistola (que es el retroceso que sufren las armas de fuego al ser disparadas), la cual reacciona ejerciendo una fuerza de igual intensidad pero en sentido contrario sobre la bala.
• La fuerza de reacción que una superficie ejerce sobre un objeto apoyado en ella, llamada fuerza normal con dirección perpendicular a la superficie.

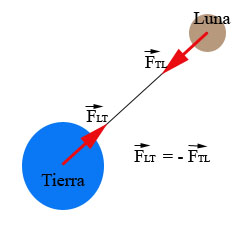
• Las fuerzas a distancia no son una excepción, como la fuerza que la Tierra ejerce sobre la Luna y viceversa, su correspondiente pareja de acción y reacción:²¹

La fuerza que ejerce la Tierra sobre la Luna es exactamente igual (y de signo contrario) a la que ejerce la Luna sobre la Tierra y su valor viene determinado por la ley de gravitación universal enunciada por Newton, que establece que la fuerza que ejerce un objeto sobre otro es directamente proporcional al producto de sus masas, e inversamente proporcional al cuadrado de la distancia que los separa. La fuerza que la Tierra ejerce sobre la Luna es la responsable de que esta no se salga de su órbita circular.
Además, la fuerza que la Luna ejerce sobre la Tierra es también responsable de las mareas, pues conforme la Luna gira alrededor de la Tierra esta ejerce una fuerza de atracción sobre la superficie terrestre, la cual eleva los mares y océanos, elevando varios metros el nivel del agua en algunos lugares; por este motivo esta fuerza también se llama fuerza de marea. La fuerza de marea de la luna se compone con la fuerza de marea del sol proporcionando el fenómeno completo de las mareas.

Limitaciones y generalizaciones posteriores

Después de que Newton formulara las tres famosas leyes, numerosos físicos y matemáticos hicieron contribuciones para darles una forma más general o de más fácil aplicación a sistemas no inerciales o a sistemas con ligaduras. Una de estas primeras generalizaciones fue el principio de d'Alembert de 1743 que era una forma válida para cuando existieran ligaduras que permitía resolver las ecuaciones sin necesidad de calcular explícitamente el valor de las reacciones asociadas a dichas ligaduras.²²
Por la misma época, Lagrange encontró una forma de las ecuaciones de movimiento válida para cualquier sistema de referencia inercial o no-inercial sin necesidad de introducir fuerzas ficticias.²³ Ya que es un hecho conocido que las Leyes de Newton, tal como fueron escritas, sólo son válidas a los sistemas de referencia inerciales, o más precisamente, para aplicarlas a sistemas no-inerciales, requieren la introducción de las llamadas fuerzas ficticias, que se comportan como fuerzas pero no están provocadas directamente por ninguna partícula material o agente concreto, sino que son un efecto aparente del sistema de referencia no inercial.²⁴
Más tarde la introducción de la teoría de la relatividad obligó a modificar la forma de la segunda ley de Newton (ver (2c)), y la mecánica cuántica dejó claro que las leyes de Newton o la relatividad general sólo son aproximaciones al comportamiento dinámico en escalas macroscópicas. También se han conjeturado algunas modificaciones macroscópicas y no-relativistas, basadas en otros supuestos como la dinámica MOND.

Generalizaciones relativistas

Las leyes de Newton constituyen tres principios aproximadamente válidos para velocidades pequeñas. La forma en que Newton las formuló no era la más general posible. De hecho la segunda y tercera leyes en su forma original no son válidas en mecánica relativista sin embargo formulados de forma ligeramente diferente la segunda ley es válida, y la tercera ley admite una formulación menos restrictiva que es válida en mecánica relativista.

• Primera ley, en ausencia de campos gravitatorios no requiere modificaciones. En un espacio-tiempo plano una línea recta cumple la condición de ser geodésica. En presencia de curvatura en el espacio-tiempo la primera ley de Newton sigue siendo correcta si sustituimos la expresión línea recta por línea geodésica.

• Segunda ley. Sigue siendo válida si se dice que la fuerza sobre una partícula coincide con la tasa de cambio de su momento lineal. Sin embargo, ahora la definición de momento lineal en la teoría newtoniana y en la teoría relativista difieren. En la teoría newtoniana el momento lineal se define según (1a) mientras que en la teoría de la relatividad de Einstein se define mediante (1b):

(1a)${\displaystyle {\mathbf {p}}=m{\mathbf {v}}}$

(1b)${\displaystyle {\mathbf {p}}={\cfrac {m{\mathbf {v}}}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}}$

donde m es la masa invariante de la partícula y ${\displaystyle {\mathbf {v}}}$ la velocidad de ésta medida desde un cierto sistema inercial. Esta segunda formulación de hecho incluye implícitamente definición (1) según la cual el momento lineal es el producto de la masa por la velocidad. Como ese supuesto implícito no se cumple en el marco de la teoría de la relatividad de Einstein (donde la definición es (2)), la expresión de la fuerza en términos de la aceleración en la teoría de la relatividad toma una forma diferente. Por ejemplo, para el movimiento rectilíneo de una partícula en un sistema inercial se tiene que la expresión equivalente a (2a) es:

(2b)${\displaystyle {\mathbf {F}}=m{\mathbf {a}}\left(1-{\frac {v^{2}}{c^{2}}}\right)^{-{\frac {3}{2}}}}$

Si la velocidad y la fuerza no son paralelas, la expresión sería la siguiente:

(2c)${\displaystyle {\mathbf {F}}={\frac {m{\mathbf {a}}}{(1-{\frac {v^{2}}{c^{2}}})^{\frac {1}{2}}}}+{\frac {m({\mathbf {v}}\cdot {\mathbf {a}}){\mathbf {v}}}{c^{2}(1-{\frac {v^{2}}{c^{2}}})^{\frac {3}{2}}}}}$

Nótese que esta última ecuación implica que salvo para el movimiento rectilíneo y el circular uniforme, el vector de aceleración y el vector de fuerza no serán parelelos y formarán un pequeño ángulo relacionado con el ángulo que formen la aceleración y la velocidad.

• Tercera Ley de Newton. La formulación original de la tercera ley por parte de Newton implica que la acción y reacción, además de ser de la misma magnitud y opuestas, son colineales. En esta forma la tercera ley no siempre se cumple en presencia de campos magnéticos. En particular, la parte magnética de la fuerza de Lorentz que se ejercen dos partículas en movimiento no son iguales y de signo contrario. Esto puede verse por cómputo directo. Dadas dos partículas puntuales con cargas q₁ y q₂ y velocidades ${\displaystyle \mathbf {v} _{i}}$, la fuerza de la partícula 1 sobre la partícula 2 es:

${\displaystyle \mathbf {F} _{12}=q_{2}\mathbf {v} _{2}\times \mathbf {B} _{1}={\frac {\mu q_{2}q_{1}}{4\pi }}\ {\frac {\mathbf {v} _{2}\times (\mathbf {v} _{1}\times \mathbf {\hat {u}} _{12})}{d^{2}}}}$

donde d la distancia entre las dos partículas y ${\displaystyle \mathbf {\hat {u}} _{12}}$ es el vector director unitario que va de la partícula 1 a la 2. Análogamente, la fuerza de la partícula 2 sobre la partícula 1 es:

${\displaystyle \mathbf {F} _{21}=q_{1}\mathbf {v} _{1}\times \mathbf {B} _{2}={\frac {\mu q_{2}q_{1}}{4\pi }}\ {\frac {\mathbf {v} _{1}\times (\mathbf {v} _{2}\times (-\mathbf {\hat {u}} _{12}))}{d^{2}}}}$

Empleando la identidad vectorial ${\displaystyle \mathbf {a} \times (\mathbf {b} \times \mathbf {c} )=(\mathbf {a} \cdot \mathbf {c} )\mathbf {b} -(\mathbf {a} \cdot \mathbf {b} )\mathbf {c} }$, puede verse que la primera fuerza está en el plano formado por ${\displaystyle \mathbf {\hat {u}} _{12}}$ y ${\displaystyle \mathbf {v} _{1}}$ que la segunda fuerza está en el plano formado por ${\displaystyle \mathbf {\hat {u}} _{12}}$ y ${\displaystyle \mathbf {v} _{2}}$. Por tanto, estas fuerzas no siempre resultan estar sobre la misma línea, ni en general son de igual magnitud

Teorema de Ehrenfest

El teorema de Ehrenfest permite generalizar las leyes de Newton al marco de la mecánica cuántica. Si bien en dicha teoría no es lícito hablar de fuerzas o de trayectoria, se puede hablar de magnitudes como momento lineal y potencial de manera similar a como se hace en mecánica newtoniana.
En concreto la versión cuántica de la segunda Ley de Newton afirma que la derivada temporal del valor esperado del momento de una partícula en un campo iguala al valor esperado de la "fuerza" o valor esperado del gradiente del potencial:

${\displaystyle {\frac {d}{dt}}\langle p\rangle =\int \Phi ^{*}V(x,t)\nabla \Phi ~dx^{3}-\int \Phi ^{*}(\nabla V(x,t))\Phi ~dx^{3}-\int \Phi ^{*}V(x,t)\nabla \Phi ~dx^{3}}$

${\displaystyle =0-\int \Phi ^{*}(\nabla V(x,t))\Phi ~dx^{3}-0=\langle -\nabla V(x,t)\rangle =\langle F\rangle ,}$

Donde:

${\displaystyle V(x,t)\,}$ es el potencial del que derivar las "fuerzas".

${\displaystyle \Phi ,\Phi ^{*}\,}$, son las funciones de onda de la partícula y su compleja conjugada.

${\displaystyle \nabla \,}$ denota el operador nabla.

Véase también

• Portal:Física. Contenido relacionado con Física.
• Sistema inercial
• Mecánica clásica
• Física clásica
• Momento de inercia
• Cantidad de movimiento
• Inercia
• Fuerza
• Choque elástico

Notas

1. 
   

Existe, además, una versión previa en un fragmento manuscrito de 1684 que lleva como título De motu corporum in mediis regulariter cedentibus. Por otro lado, en ese mismo texto queda claro que, originalmente, Newton había propuesto cinco leyes, de las cuales la cuarta era el principio de relatividad de Galileo.

Los primeros esfuerzos registrados por el ser humano para reunir sistemáticamente el conocimiento sobre el movimiento de los cuerpos proceden de la antigua Grecia. En la filosofía natural establecida por Aristóteles las explicaciones de los fenómenos físicos se deducían de la hipótesis sobre el mundo y no de la experimentación.

Soto destaca sin duda como un magnífico profesor, el mejor simplificador en la clasificación de los movimientos, y quien más interesado estaba en unificar las formulaciones abstractas con el mundo físico real.

Domingo de Soto había formulado más de cincuenta años atrás que el movimiento de caída era un movimiento uniformemente acelerado, unijórmiter disformis con respecto al tiempo. Y ese era el principio que Galileo necesitaba.

Un avance muy importante se debió a Galileo (1564-1642) quien introdujo el método científico, que enseña que no siempre se debe creer en las conclusiones intuitivas basadas en la observación inmediata, pues esto lleva a menudo a equivocaciones. Galileo realizó un gran número de experiencias en las que se iban cambiando ligeramente las condiciones del problema y midió los resultados en cada caso. De esta manera pudo extrapolar sus observaciones hasta llegar a entender un experimento ideal.

6. Fue Isaac Newton (hacia 1690) el primero en dar una formulación completa de las leyes de la mecánica e inventó los procedimientos matemáticos necesarios para explicarlos y obtener información a partir de ellos.

Referencias

1. 
   

Pickover, 2009, pp. 132-170.

Dudley Williams y John Spangler, Physics for Science and Engineering, ápud Pickover (2009, pp. 133)

Medina Domínguez, Alejandro; Ovejero Sánchez, Jesús. «Leyes de Newton y sus aplicaciones». Física I. Curso 2010/11.

Tipler y Mosca, 2006, pp. 4.

Navarro, Víctor. «Juan de Celaya». mcnbiografias.com. Consultado el 16 de mayo de 2015.

Battaner, Eduardo (2011). Física de las Noches Estrelladas. Tusquets. ISBN 9788483833421. «Todos los países tienen la tendencia a atribuir a algunos de sus pretéritos hijos los grandes descubrimientos. Nosotros parece que no. Menéndez Pelayo nos cuenta que Juan de Celaya era escolástico degenerado, recalcitrante y bárbaro. ¡Injustos epítetos para el científico que enunció por primera vez una de las leyes más importantes de la Física!»

Navarro, Víctor. «Domingo de Soto». mcnbiografias.com. Consultado el 16 de mayo de 2015.

Pérez Camacho, Juan José; Sols Lucía, Ignacio (1994). «Domingo de Soto en el origen de la ciencia moderna». Revista de filosofía (12): 455-476. ISSN 0034-8244. Consultado el 16 de mayo de 2015.

de Soto, Domingo. «7». Quaestiones.

Dugas, Rene; Costabel, Pierre (2008). «La escuela inglesa desde Descartes hasta Newton». Newton. Vida, pensamiento y obra: 116-131.

Newton Leges (The Latin Library)

Rada García, Eloy (trad.) (2003). «Principios matemáticos de la filosofía natural». apud. Newton. Vida, pensamiento y obra, pág. 199. A hombros de gigantes. Las grandes obras de la física y la Astronomía (Barcelona: Crítica).

Isaac Newton, extractos de Principios matemáticos de la filosofía natural, cit., pág. 199.

M. Sebastiá, José Sebastiá (2013). «Las Leyes de Newton de la mecánica». En Universidad Simón Bolívar. Didáctica de las ciencias experimentales y sociales (27): 210. ISSN 0214-4379. Consultado el 9 de julio de 2015.

Departamento de Física Aplicada III. Universidad de Sevilla (ed.). «Propiedades de un sistema de partículas». Laplace.

Tipler y Mosca, 2006, pp. 230.

Tipler y Mosca, 2006, pp. 207.

Tipler y Mosca, 2006, pp. 217.

Pickover, 2009, p. 137.

Tipler y Mosca, 2006, pp. 98.

Tipler y Mosca, 2006, pp. 87.

A. Fernández Rañanada: Dinámica clásica, pp. 131-33.

A. Fernández Rañanada: Dinámica clásica, pp. 102-09.

24. A. Fernández Rañanada: Dinámica clásica, pp. 366-75.

Bibliografía

• Alonso, Marcelo; Finn, Edward J. (1998). Física 1. Madrid. ISBN 9789684442238.
• Bell, Eric T. (1986). On the Seashore: Newton (en inglés). ISBN 978-0671628185.
• Christianson, Gale E. (1985). In the Presence of the Creator: Isaac Newton and His Times (en inglés). ISBN 978-0029051900.
• Da Costa Andrade, Edward N. (1979). Sir Isaac Newton (en inglés). ISBN 978-0313220227.
• De Gandt, François (2014). Force and Geometry in Newton's "Principia" (Princeton Legacy Library) (en inglés). ISBN 978-0691033679.
• De Juana, José María (2003). Física General 1. Pearson Prentice Hall. ISBN 84-205-3342-4.
• Fauvel, John; Flood, Raymond; Shortland, Michael; Wilson, Robin (1988). Let Newton Be! (en inglés). ISBN 978-0198539247.
• Ortega Girón, Manuel R. (1989-2010). Lecciones de Física (4 volúmenes). Monytex. ISBN 84-404-4290-4.
• Pickover, Clifford A. (2009). De Arquímedes a Hawking. Las leyes de la ciencia y sus descubridores. Barcelona: Crítica. ISBN 978-84-9892-003-1.
• Sagan, Carl (1981). Cosmos. ISBN 2-86374-075-X.
• Sears, W.; Zemansky, M.W.; Young, H.D.; Freedman, F. (1999). Física Universitaria 1. Addison-Wesley-Longman. ISBN 968-444-277-7.
• Tipler, Paul Allen; Mosca, Gene (2006). Física para la ciencia y la tecnología 2. Reverté. ISBN 8429144129.
• Tippens, Paul E. (2007). Física Concepto y aplicaciones. México: McGraw-Hill. ISBN 9789701062609.
• Westfall, Richard S. (1983). Never at Rest: A Biography of Isaac Newton (Cambridge Paperback Library) (en inglés). ISBN 978-0521274357.
• Zitzewitz, Paul W.; Neff, Robert F. (1995). Física 1. McGraw-Hill. ISBN 978-958-600-381-0.

Enlaces externos

• Evolución histórica de la relación fuerza-movimiento
• Segunda ley de Newton. Relación entre fuerza y aceleración
• Dinámica de una partícula
• Newton’s Life (en inglés)
• « Lois de Newton » (en francés).