En física, la energía cinética de un cuerpo es aquella energía que posee debido a su movimiento. Se define como el trabajonecesario para acelerar un cuerpo de una masa determinada desde el reposo hasta la velocidad indicada. Una vez conseguida esta energía durante la aceleración, el cuerpo mantiene su energía cinética salvo que cambie su velocidad. Para que el cuerpo regrese a su estado de reposo se requiere un trabajo negativo de la misma magnitud que su energía cinética. Suele abreviarse con letra E- oE+ (a veces también T o K).
Índice
[ocultar]Introducción[editar]
El adjetivo «cinético» en el nombre energía viene de la antigua palabra griega κίνησις, kinesis, que significa «movimiento». Los términos energía cinética y trabajo y su significado científico provienen del siglo XIX.
El principio de la mecánica clásica que E α mv ² fue desarrollado por primera vez por Gottfried Leibniz y Daniel Bernoulli , que describe la energía cinética como la fuerza viva ovis viva. Willem 's Gravesande de los Países Bajos proporcionó evidencia experimental de esta relación. Al caer los pesos de diferentes alturas en un bloque de arcilla, Gravesande determinó que la profundidad de penetración es proporcional al cuadrado de la velocidad de impacto. Émilie du Châtelet reconoció las implicaciones del experimento y publicó una explicación.
Los primeros conocimientos de esas ideas pueden ser atribuidos a Gaspard Coriolis quien en 1829 publicó un artículo titulado Du Calcul de l'Effet des Machines esbozando las matemáticas de la energía cinética. El término energía cinética se debe a William Thomson más conocido como Lord Kelvin en 1849.
Existen varias formas de energía como la energía química, el calor, la radiación electromagnética, la energía nuclear, las energías gravitacional, eléctrica, elástica, etc, todas ellas pueden ser agrupadas en dos tipos: la energía potencial y la energía cinética.
La energía cinética puede ser entendida mejor con ejemplos que demuestren cómo esta se transforma de otros tipos de energía y a otros tipos de energía. Por ejemplo un ciclista quiere usar la energía química que le proporcionó su comida para acelerar su bicicleta a una velocidad elegida. Su velocidad puede mantenerse sin mucho trabajo, excepto por la resistencia del aire y la fricción. La energía química es convertida en una energía de movimiento, conocida como energía cinética, pero el proceso no es completamente eficiente y el ciclista también produce calor.
La energía cinética en movimiento de la bicicleta y el ciclista pueden convertirse en otras formas. Por ejemplo, el ciclista puede encontrar una cuesta lo suficientemente alta para subir, así que debe cargar la bicicleta hasta la cima. La energía cinética hasta ahora usada se habrá convertido en energía potencial gravitatoria que puede liberarse lanzándose cuesta abajo por el otro lado de la colina. Alternativamente el ciclista puede conectar una dínamo a una de sus ruedas y así generar energía eléctrica en el descenso. La bicicleta podría estar viajando más despacio en el final de la colina porque mucha de esa energía ha sido desviada en hacer energía eléctrica. Otra posibilidad podría ser que el ciclista aplique sus frenos y en ese caso la energía cinética se estaría disipando a través de la fricción en energía calórica.
Como cualquier magnitud física que sea función de la velocidad, la energía cinética de un objeto no solo depende de la naturaleza interna de ese objeto, también depende de la relación entre el objeto y el observador (en física un observador es formalmente definido por una clase particular de sistema de coordenadas llamado sistema inercial de referencia). Magnitudes físicas como esta son llamadas invariantes. La energía cinética esta co-localizada con el objeto y atribuido a ese campo gravitacional.
El cálculo de la energía cinética se realiza de diferentes formas según se use la mecánica clásica, la mecánica relativista o la mecánica cuántica. El modo correcto de calcular la energía cinética de un sistema depende de su tamaño, y la velocidad de las partículas que lo forman. Así, si el objeto se mueve a una velocidad mucho más baja que la velocidad de la luz, la mecánica clásica de Newton será suficiente para los cálculos; pero si la velocidad es cercana a la velocidad de la luz, la teoría de la relatividad empieza a mostrar diferencias significativas en el resultado y debería ser usada. Si el tamaño del objeto es más pequeño, es decir, de nivel subatómico, la mecánica cuántica es más apropiada.
Esta energía se degrada y se conserva en cada transformación, perdiendo capacidad de realizar nuevas transformaciones, pero la energía no puede ser creada ni destruida, sólo transformada, por lo que la suma de todas las energías en el universo es siempre constante. Un objeto perderá energía en una transformación, pero esa pérdida de energía irá a parar a otro sitio, por ejemplo se puede transformar en calor.
Energía cinética en mecánica clásica[editar]
Energía cinética en diferentes sistemas de referencia[editar]
Como hemos dicho, en la mecánica clásica, la energía cinética de una masa puntual depende de su masa  y sus componentes del movimiento. Se expresa en Joule (J). 1 J = 1 kg·m2/s2. Estos son descritos por la velocidad
y sus componentes del movimiento. Se expresa en Joule (J). 1 J = 1 kg·m2/s2. Estos son descritos por la velocidad  de la masa puntual, así:
de la masa puntual, así: 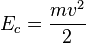
 y sus componentes del movimiento. Se expresa en Joule (J). 1 J = 1 kg·m2/s2. Estos son descritos por la velocidad
y sus componentes del movimiento. Se expresa en Joule (J). 1 J = 1 kg·m2/s2. Estos son descritos por la velocidad  de la masa puntual, así:
de la masa puntual, así: 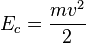
En un sistema de coordenadas especial, esta expresión tiene las siguientes formas:
- Coordenadas cartesianas (x, y, z):
Con eso el significado de un punto en una coordenada y su cambio temporal se describe como la derivada temporal de su desplazamiento:
En un formalismo hamiltoniano no se trabaja con esas componentes del movimiento, o sea con su velocidad, sino con su impulso  (cambio en la cantidad de movimiento). En caso de usar componentes cartesianas obtenemos:
(cambio en la cantidad de movimiento). En caso de usar componentes cartesianas obtenemos:
 (cambio en la cantidad de movimiento). En caso de usar componentes cartesianas obtenemos:
(cambio en la cantidad de movimiento). En caso de usar componentes cartesianas obtenemos:Energía cinética de sistemas de partículas[editar]
Para una partícula, o para un sólido rígido que no este rotando, la energía cinética cae a cero cuando el cuerpo para. Sin embargo, para sistemas que contienen muchos cuerpos con movimientos independientes, que ejercen fuerzas entre ellos y que pueden (o no) estar rotando, esto no es del todo cierto. Esta energía es llamada 'energía interna'. La energía cinética de un sistema en cualquier instante de tiempo es la suma simple de las energías cinéticas de las masas, incluyendo la energía cinética de la rotación.
Un ejemplo de esto puede ser el Sistema Solar. En el centro de masas del sistema solar, el Sol está (casi) estacionario, pero los planetas y planetoides están en movimiento sobre él. Así en un centro de masas estacionario, la energía cinética está aún presente. Sin embargo, recalcular la energía de diferentes marcos puede ser tedioso, pero hay un truco. La energía cinética de un sistema de diferentes marcos inerciales puede calcularse como la simple suma de la energía en un marco con centro de masas y añadir en la energía el total de las masas de los cuerpos que se mueven con velocidad relativa entre los dos marcos.
Esto se puede demostrar fácilmente: sea V la velocidad relativa en un sistema k de un centro de masas i:
Donde:
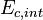 , es la energía cinética interna respecto al centro de masas de ese sistema
, es la energía cinética interna respecto al centro de masas de ese sistema es el momento respecto al centro de masas, que resulta ser cero por la definición de centro de masas.
es el momento respecto al centro de masas, que resulta ser cero por la definición de centro de masas. , es la masa total.
, es la masa total.
Por lo que la expresión anterior puede escribirse simplemente como:1
Donde puede verse más claramente que energía cinética total de un sistema puede descomponerse en su energía cinética de traslación y la energía de rotación alrededor del centro de masas. La energía cinética de un sistema entonces depende del Sistema de referencia inercial y es más bajo con respecto al centro de masas referencial, por ejemplo, en un sistema de referencia en que el centro de masas sea estacionario. En cualquier otro sistema de referencia hay una energía cinética adicional correspondiente a la masa total que se mueve a la velocidad del centro de masas.
Energía cinética de un sólido rígido en rotación[editar]
Para un sólido rígido que está rotando puede descomponerse la energía cinética total como dos sumas: la energía cinética de traslación (que es la asociada al desplazamiento del centro de masa del cuerpo a través del espacio) y la energía cinética de rotación (que es la asociada al movimiento de rotación con cierta velocidad angular). La expresión matemática para la energía cinética es:
Donde:
 Energía de traslación.
Energía de traslación.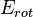 Energía de rotación.
Energía de rotación. Masa del cuerpo.
Masa del cuerpo. tensor de (momentos de) inercia.
tensor de (momentos de) inercia. velocidad angular del cuerpo.
velocidad angular del cuerpo. traspuesta del vector de la velocidad angular del cuerpo.
traspuesta del vector de la velocidad angular del cuerpo. velocidad lineal del cuerpo.
velocidad lineal del cuerpo.
El valor de la energía cinética es positivo, y depende del sistema de referencia que se considere al determinar el valor (módulo) de la velocidad  y
y  . La expresión anterior puede deducirse de la expresión general:
. La expresión anterior puede deducirse de la expresión general:
 y
y  . La expresión anterior puede deducirse de la expresión general:
. La expresión anterior puede deducirse de la expresión general:Energía cinética en mecánica relativista[editar]
Energía cinética de una partícula[editar]
Si la velocidad de un cuerpo es una fracción significante de la velocidad de la luz, es necesario utilizar mecánica relativista para poder calcular la energía cinética. Enrelatividad especial, debemos cambiar la expresión para el momento lineal y de ella por interacción se puede deducir la expresión de la energía cinética:
Tomando la expresión relativista anterior, desarrollándola en serie de Taylor y tomando únicamente el término  se recupera la expresión de la energía cinética típica de la mecánica newtoniana:2
se recupera la expresión de la energía cinética típica de la mecánica newtoniana:2
 se recupera la expresión de la energía cinética típica de la mecánica newtoniana:2
se recupera la expresión de la energía cinética típica de la mecánica newtoniana:2
Se toma únicamente el primer término de la serie de Taylor ya que, conforme la serie progresa, los términos se vuelven cada vez más y más pequeños y es posible despreciarlos.
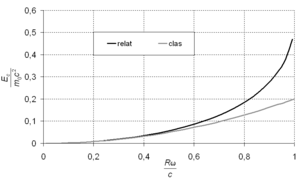
La ecuación relativista muestra que la energía de un objeto se acerca al infinito cuando la velocidad v se acerca a la velocidad de la luz c, entonces es imposible acelerar un objeto a esas magnitudes. Este producto matemático es la fórmula de equivalencia entre masa y energía, cuando el cuerpo está en reposo obtenemos esta ecuación:
Así, la energía total E puede particionarse entre las energías de las masas en reposo más la tradicional energía cinética newtoniana de baja velocidad. Cuando los objetos se mueven a velocidades mucho más bajas que la luz (ej. cualquier fenómeno en la tierra) los primeros dos términos de la serie predominan.
La relación entre energía cinética y momentum es más complicada en este caso y viene dada por la ecuación:
Esto también puede expandirse como una serie de Taylor, el primer término de esta simple expresión viene de la mecánica newtoniana. Lo que sugiere esto es que las fórmulas para la energía y el momento no son especiales ni axiomáticas pero algunos conceptos emergen de las ecuaciones de masa con energía y de los principios de la relatividad.
Energía cinética de un sólido en rotación[editar]
A diferencia del caso clásico la energía cinética de rotación en mecánica relativista no puede ser representada simplemente por un tensor de inercia y una expresión cuadrática a partir de él en el que intervenga la velocidad angular. El caso simple de una esfera en rotación ilustra este punto; si suponemos una esfera de un material suficientemente rígido para que podamos despreciar las deformaciones por culpa de la rotación (y por tanto los cambios de densidad) y tal que su velocidad angular satisfaga la condición 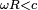 se puede calcular la energía cinética
se puede calcular la energía cinética  a partir de la siguiente integral:
a partir de la siguiente integral:
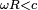 se puede calcular la energía cinética
se puede calcular la energía cinética  a partir de la siguiente integral:
a partir de la siguiente integral:
Integrando la expresión anterior se obtiene la expresión:
Para una esfera en rotación los puntos sobre el eje no tienen velocidad de traslación mientras que los puntos más alejados del eje de giro tienen una velocidad  , a medida que esta velocidad se aproxima a la velocidad de la luz la energía cinética de la esfera tiende a crecer sin límite. Esto contrasta con la expresión clásica que se da a continuación:
, a medida que esta velocidad se aproxima a la velocidad de la luz la energía cinética de la esfera tiende a crecer sin límite. Esto contrasta con la expresión clásica que se da a continuación:
 , a medida que esta velocidad se aproxima a la velocidad de la luz la energía cinética de la esfera tiende a crecer sin límite. Esto contrasta con la expresión clásica que se da a continuación:
, a medida que esta velocidad se aproxima a la velocidad de la luz la energía cinética de la esfera tiende a crecer sin límite. Esto contrasta con la expresión clásica que se da a continuación:
Paradójicamente, dentro de la teoría especial de la relatividad, el supuesto de que es posible construir un sistema rotar progresivamente más rápido un esfera sobre su eje, lleva a que los puntos más alejados del eje de giro alcancen la velocidad de la luz aplicando al cuerpo una cantidad finita de energía 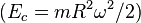 . Lo cual revela que el supuesto no puede ser correcto cuando algunos puntos de la periferia del sólido están moviéndose a velocidades cercanas a la de la luz.
. Lo cual revela que el supuesto no puede ser correcto cuando algunos puntos de la periferia del sólido están moviéndose a velocidades cercanas a la de la luz.
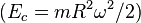 . Lo cual revela que el supuesto no puede ser correcto cuando algunos puntos de la periferia del sólido están moviéndose a velocidades cercanas a la de la luz.
. Lo cual revela que el supuesto no puede ser correcto cuando algunos puntos de la periferia del sólido están moviéndose a velocidades cercanas a la de la luz.Energía cinética en mecánica cuántica[editar]
En la mecánica cuántica, el valor que se espera de energía cinética de un electrón, 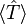 , para un sistema de electrones describe una función de onda
, para un sistema de electrones describe una función de onda 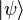 que es la suma de un electrón, el operador se espera que alcance el valor de:
que es la suma de un electrón, el operador se espera que alcance el valor de:
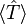 , para un sistema de electrones describe una función de onda
, para un sistema de electrones describe una función de onda 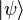 que es la suma de un electrón, el operador se espera que alcance el valor de:
que es la suma de un electrón, el operador se espera que alcance el valor de:
donde 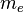 es la masa de un electrón y
es la masa de un electrón y 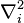 es el operador laplaciano que actúa en las coordenadas del electrón iésimo y la suma de todos los otros electrones. Note que es una versión cuantizada de una expresión no relativista de energía cinética en términos de momento:
es el operador laplaciano que actúa en las coordenadas del electrón iésimo y la suma de todos los otros electrones. Note que es una versión cuantizada de una expresión no relativista de energía cinética en términos de momento:
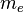 es la masa de un electrón y
es la masa de un electrón y 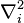 es el operador laplaciano que actúa en las coordenadas del electrón iésimo y la suma de todos los otros electrones. Note que es una versión cuantizada de una expresión no relativista de energía cinética en términos de momento:
es el operador laplaciano que actúa en las coordenadas del electrón iésimo y la suma de todos los otros electrones. Note que es una versión cuantizada de una expresión no relativista de energía cinética en términos de momento:
El formalismo de la funcional de densidad en mecánica cuántica requiere un conocimiento sobre la densidad electrónica, para esto formalmente no se requiere conocimientos de la función de onda.
Dado una densidad electrónica 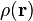 , la funcional exacta de la energía cinética del n-ésimo electrón es incierta; sin embargo, en un caso específico de un sistema de un electrón, la energía cinética puede escribirse así:
, la funcional exacta de la energía cinética del n-ésimo electrón es incierta; sin embargo, en un caso específico de un sistema de un electrón, la energía cinética puede escribirse así:
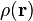 , la funcional exacta de la energía cinética del n-ésimo electrón es incierta; sin embargo, en un caso específico de un sistema de un electrón, la energía cinética puede escribirse así:
, la funcional exacta de la energía cinética del n-ésimo electrón es incierta; sin embargo, en un caso específico de un sistema de un electrón, la energía cinética puede escribirse así:
donde ![T[\rho]](https://upload.wikimedia.org/math/b/0/3/b03e2e33686044e5f78fe6df092b3bd0.png) es conocida como la funcional de la energía cinética de Von Weizsacker.
es conocida como la funcional de la energía cinética de Von Weizsacker.
![T[\rho]](https://upload.wikimedia.org/math/b/0/3/b03e2e33686044e5f78fe6df092b3bd0.png) es conocida como la funcional de la energía cinética de Von Weizsacker.
es conocida como la funcional de la energía cinética de Von Weizsacker.Energía cinética de partículas en la mecánica cuántica[editar]
En la teoría cuántica una magnitud física como la energía cinética debe venir representada por un operador autoadjunto en un espacio de Hilbert adecuado. Ese operador puede construirse por un proceso de cuantización, el cual conduce para una partícula moviéndose por el espacio euclidiano tridimensional a una representación natural de ese operador sobre el espacio de Hilbert 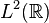 dado por:
dado por:
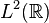 dado por:
dado por:
que, sobre un dominio denso de dicho espacio formado clases de equivalencia representables por funciones C², define un operador autoadjunto con autovalores siempre positivos, lo cual hace que sean interpretables como valores físicamente medibles de la energía cinética.
Energía cinética del sólido rígido en la mecánica cuántica[editar]
Un sólido rígido a pesar de estar formado por un número infinito de partículas, es un sistema mecánico con un número finito de grados de libertad lo cual hace que su equivalente cuántico pueda ser representado por sobre un espacio de Hilbert de dimensión infinita de tipo L² sobre un espacio de configuración de inútiles dimensión finita. En este caso el espacio de configuración de un sólido rígido es precisamente el grupo de Lie SO(3) y por tanto el espacio de Hilbert pertinente y el operador energía cinética de rotación pueden representarse por:
donde  es la medida de Haar invariante de SO(3),
es la medida de Haar invariante de SO(3), 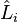 son los operadores del momento angular en la representación adecuada y los escalares
son los operadores del momento angular en la representación adecuada y los escalares 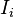 son los momentos de inercia principales.
son los momentos de inercia principales.
 es la medida de Haar invariante de SO(3),
es la medida de Haar invariante de SO(3), 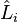 son los operadores del momento angular en la representación adecuada y los escalares
son los operadores del momento angular en la representación adecuada y los escalares 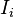 son los momentos de inercia principales.
son los momentos de inercia principales.Energía cinética y temperatura[editar]
A nivel microscópico la energía cinética promedio de las moléculas de un gas define su temperatura. De acuerdo con la ley de Maxwell-Boltzmann para un gas ideal clásico la relación entre la temperatura absoluta (T) de un gas y su energía cinética media es:
Véase también[editar]
- Masa inercial
- Energía potencial
- Energía mecánica
- Movimiento browniano
- Teorema de la energía cinética
- Vis viva
- Energía eólica
Referencias[editar]
- ↑ Center of Mass Reference Frame
- ↑ Resnick, R.; Halliday, D.; Krane, K. S. (2001). «Trabajo y energía». Física Vol. 1 (4ª edición en inglés; en español, 3ª edición). compañía Editorial Mexicana; John Wiley and Sons Inc. p. 162. ISBN 968-26-1230-6.
Bibliografía[editar]
- Serway, Raymond A.; Jewett, John W. (2004). Physics for Scientists and Engineers (6th ed. edición). Brooks/Cole. ISBN 0-534-40842-7.
- Tipler, Paul (2004). Physics for Scientists and Engineers: Mechanics, Oscillations and Waves, Thermodynamics (5th ed. edición). W. H. Freeman. ISBN 0-7167-0809-4.
- Tipler, Paul; Llewellyn, Ralph (2002). Modern Physics (4th ed. edición). W. H. Freeman. ISBN 0-7167-4345-0.
Enlaces externos[editar]
 Wikcionario tiene definiciones y otra información sobre energía cinética.
Wikcionario tiene definiciones y otra información sobre energía cinética.



 ):
):
 ):
):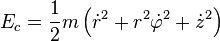
 ):
):![E_c=\frac{1}{2}m \left(r^2 \left[\dot \theta^2 + \dot \varphi^2 \sin^2\theta \right] + \dot r^2 \right)](https://upload.wikimedia.org/math/1/b/6/1b63189e3cca32b06f6f4ede5a1bf61b.png)
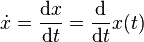


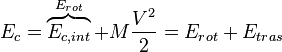
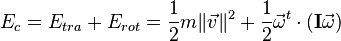
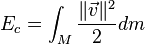
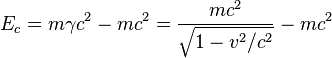
![E_c = \frac{mc^2}{\sqrt{1-\frac{v^2}{c^2}}}-mc^2=
mc^2\left [\frac{1}{2}\left(\frac{v^2}{c^2}\right)+
\frac{3}{8}\left(\frac{v^2}{c^2}\right)^2+...\right] = \frac{1}{2}mv^2](https://upload.wikimedia.org/math/a/7/0/a707bed31a55d4d79c8be7b5e9db66a4.png)

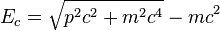

![E_c = \frac{3}{2}m_0c^2 \left(\frac{c}{R\omega}\right)^2
\left[ 1 + \frac{1}{2} \left(\frac{R\omega}{c}-\frac{c}{R\omega}\right)
\ln \left(\frac{c+R\omega}{c-R\omega} \right) \right]
- m_0c^2](https://upload.wikimedia.org/math/8/b/7/8b7a701ef31b6f0f0083d4d0260a4ca4.png)
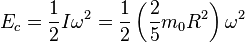
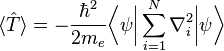
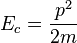
![T[\rho] = \frac{1}{8} \int \frac{ \nabla \rho(\mathbf{r}) \cdot \nabla \rho(\mathbf{r}) }{ \rho(\mathbf{r}) } d^3r](https://upload.wikimedia.org/math/f/5/2/f527c2275e20ee9262c65527e0d16fe9.png)

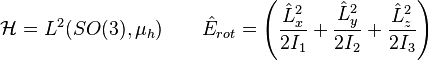

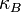 es la
es la 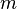 es la
es la
No hay comentarios:
Publicar un comentario
Procura comentar con libertad y con respeto. Este blog es gratuito, no hacemos publicidad y está puesto totalmente a vuestra disposición. Pero pedimos todo el respeto del mundo a todo el mundo. Gracias.